Quantum Mechanics
Created | Updated May 28, 2007
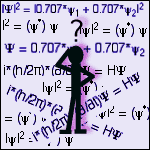
Quantum Mechanics is the branch of science that deals with extremely small particles. These particles are so incredibly small that they lie completely outside the realm of human experience. Fundamentally, this is why the ideas of quantum mechanics seem so bizarre to us. One of the most beautiful aspects of quantum mechanics is that when the equations are applied to 'normal' sized objects (ie, a bowling ball), you get the same results as you would with Newton's Laws of Motion1.
Problems in quantum mechanics seem to be much more difficult than those in classical (Newtonian) mechanics; but, in general, the judging committee is somewhat biased. Everyone grows up learning classical mechanics from everyday experiences, and this gives us a powerful intuition from which we can start to think about more abstract classical mechanics problems. It is much easier to describe how a building holds up during a hurricane or why helicopters can hover, because everyone has experienced gravity and is familiar with concepts like strength, hardness, wind, etc. It is much more difficult to explain the quantum analogue - for example, why atoms emit radiation, or how molecules form from atoms. This is due to the fact that the properties and behaviour of electrons and nuclei (the building blocks of atoms and molecules) are completely foreign to our everyday experience.
The difference between quantum and classical mechanics can be summed up very succinctly. Newton assumed that the position and velocity of any object could be defined with arbitrary precision. This assumption works extremely well for macroscopic objects - like the previously referenced bowling ball. However, there is no basis for this assumption outside of our empirical everyday experiences! Quantum mechanics is simply a formulation of mechanics in which the assumption of arbitrary precision has been thrown out. The consequences, however startling, all derive from this new statement of finite precision. The finite precision is not a result of our inability to make precise measurements; it is a fundamental fact about the nature of particles. The exact extent to which precision is limited is quantified by Heisenberg's Uncertainty Principle.
Tunnelling - an Example
There is a quantum phenomenon known as tunnelling, which states that it is possible for a particle to end up on the opposite side of a barrier even if it doesn't have enough energy to pass over the barrier. The classical mechanics analogue would involve riding a roller coaster, in which the operator didn't give it enough speed to reach the top of the track. In the classical mechanics world, the coaster would stop near the top (at a point known as the 'classical turning point'), and roll backwards. In the quantum world there is a chance that the 'roller coaster'2, would appear on the other side of the crest, at which point it would begin to roll forward as if nothing unusual had just happened.
This is a quintessential example of a bizarre quantum phenomenon that has no classical analogue. However, it is easily understood in the context of finite precision of the velocity of the roller coaster. If, for some reason, we were unsure of the velocity that the operator initially gave the coaster, maybe by about plus or minus 10 km/hr, then we would be unable to say whether the coaster was going reach the top and continue, or merely stop and roll backwards. We could make a guess, based on the most probable velocity of the coaster, as to whether or not the coaster would reach the top or fall back, but we couldn't say for certain one way or the other. This is exactly the cause of tunneling in the quantum world: the uncertainty in the velocity (or energy) of a particle makes it possible for an event that should be impossible to occur. Another critical feature of the tunneling problem is the fact that after the tunneling event has occurred, the uncertainty in the coaster's velocity would remain. Intuitively we think that we should know some information about the coaster's velocity if it made it up the other side of the peak, but that is not the case quantum mechanically because the uncertainty in the velocity is fundamental to the nature of all particles!
The Maths of Probability
The rest of quantum mechanics is just the maths necessary to describe events in terms of probabilities, instead of certainties. There is, however, a direct mathematical connection to classical mechanics, given by Ehrenfest's Theorem. According to this theorem, the maximum limit of the probability distribution for a particle obeys Newton's Laws of Motion. Ehrenfest's theorem is the exact mathematical statement of why quantum mechanics works exactly the same as classical mechanics when applied to large objects. This is a huge boon to people who use quantum mechanics, as it allows them to step back and use their intuition from the classical mechanics world. However, most of the interesting quantum mechanics comes from the shape of the probability distribution, not just the peak, so it is critically important to use the exact quantum formalism when dealing with microscopic particles. It is amazing how much more difficult it is to work with probabilities, but it doesn't appear as if there is any viable alternative. Although many other theories have been proposed to replace quantum mechanics, all have either failed when confronted by experiment, or have proven to be even more cumbersome mathematically.
Advanced Concepts in Quantum Mechanics
The goal of this section is to very briefly go over some of the maths involved in quantum mechanics. It will not cover the points described above, but is mainly designed to give anyone who remembers their classical mechanics a feel for why quantum mechanical calculations can be so much harder than their classical mechanical equivalents.
The big scientific theories are usually composed of laws or postulates. Quantum mechanics is no different. In order to explain these postulates, let's imagine an electron whose motion is confined to some arbitary space. The most common example of this would be the electrons that are in plain, everyday atoms. This confined electron will be our "system". The classical mechanics equivalent of this system would be a marble in a large mixing bowl. The marble can roll around in the bowl with all kinds of interesting motion, and will even fly out of the bowl if it gets rolling fast enough. These systems will be critical in explaining the main posulates of quantum mechanics3:
The fundamental idea behind all quantum mechanics is the concept of using eigenstates to describe systems. There are three main points to make about eigenstates:
The energy, velocity, position, etc. of the system is defined by its eigenstates. The energy (and other observables) of each eigenstate usually can only take on discrete, non-continuous values. In the case of our electron, there could be two eigenstates, one with an energy of 1 eV4, and another with an energy of 2.5 eV. There would be no eigenstates associated with any other values of the energy. The energy of the electron is then said to be quantized5.
Each eigenstate has associated with it a stationary state wavefunction, ψ. There would be one wavefunction for each of the values of the energy listed above (ψ1 and ψ2). The square of the wavefunction |ψ|2 gives the probability distribution of the eigenstate. The vertical lines denote a special form of squaring:
|ψ|2 = (ψ*) ψ
where ψ* is the complex-conjugate of ψ6. For example, if the vector r denotes the position of the marble within the bowl, or the electron within the atom, then the wavefunction for the marble would be ψ(r). The probability of finding the marble (or electron) at a given location would be given by |ψ(r)|2. The integral of this function over all space must be 1. This condition is known as normalisation and it is a simple mathematical requirement of any probability distribution - it is the result of the definition of probability.The current state of the system is defined by any linear combination of the eigenstates. This new wavefunction is known as a superposition state. Using our eigenstate wavefunctions from above, a superposition of the system could be defined as:
Ψ = 0.707*ψ1 + 0.707*ψ2
The probability function for this superposition state is given by:|Ψ|2 = |0.707*ψ1 + 0.707*ψ2|2
Since this is still a probability distribution, the laws of probability still hold, and it too must be normalized. The odd-looking decimal coefficients are a result of the normalization condition. This state actually corresponds to an equal mixture of the two eigenstates.
Physical quantities, such as energy, velocity, position, etc. are determined from wavefunctions by the use of operators7. Operators are the equivalent of mathematical commands - for example "take the derivate with respect to x" is an operator. The most important operator in quantum mechanics is the energy operator, also known as the Hamiltonian (denoted H). As the name implies, this operator is used to calculate the energy of the system. The actual calculation of a physical quantity involves sandwiching the operator into the probability distribution of the system, and then integrating over all space. This gives the expected value of the physical quantity, or "expectation" value. The expectation value of the energy would be denoted as <E> and it would be calculated using:
<E> = ∫ψ*Hψ dr
When carrying out an actual experiment, individual measurements will only yield physically observable quantities corresponding to the discrete eigenvalues of one of the possible eigenstates of the system. In the case of our electron in a superposition state, a single measurement of the energy will only yield either a value of 1 or 2.5 eV. This is where the idea of quantization of the electron's energy is actually observed. Usually what happens is that a large number of measurements are made repeatedly on the system, or one measurement is made on a large number of identical systems. In this scenario, the quantization is washed out, and the average energy (1.75 eV in the case of the superposition state above) is observed.
The probability of observing one of the allowed energies from the superposition state is given by the square of the coefficient of the corresponding eigenstate. In our example, the coefficient of each state is 0.707, and since (0.707)2 = 0.5, the probability of measuring each energy is ½. In this case measuring the values of the energy is the same as flipping a coin - heads means 1 eV, tails means 2.5 eV.
After carrying out a measurement on a superposition state, the system will no longer be in the superposition state. Instead it will be in the eigenstate corresponding to the eigenvalue that was just measured. In our example, if we measure our system to have an energy of 1 eV, then the system after the measurement is only in the eigenstate which has the wavefunction *ψ1. Repeated measurements of the exact same system will forever after only yield the energy of 1 eV.
The superposition state (and thus the system) evolves in time according to the Schrodinger equation:
i*(h/2π)*(∂/∂t)Ψ = HΨ
where i is the imaginary number8, h is Planck's constant, π is the irrational number pi, ∂/∂t is the derivative with respect to time, Ψ is the superposition state, and H is the Hamiltonian (energy) operator. Usually this equation must be solved numerically by very large computers for all but the most simple cases.
These are the rules which physicists apply to tiny particles to achieve the dazzling and mind-boggling effects of quantum mechanics. Most of them have fairly simple mathematical representations; but, unfortunately, the mathematical quantities being described lie far outside of our everyday experiences.

